- 11 April 2023
- Prof. Giovanni Acampora
- Dr. Autilia Vitiello
The need for a new community in quantum artificial intelligence
Quantum computing is an emerging computing paradigm that has captured the attention of researchers and practitioners due to its potential ability to enable the design of algorithms that solve hard problems more efficiently than their classical counterparts. This potentiality was proven in 1994 by Peter Shor, who designed an efficient quantum algorithm for factoring integers numbers [1]. Indeed, with respect to the classical computation applied to the problem of the integer factorization, there is no algorithm able to compute all factors of an integer number n in a polynomial time O(bk), where b is the number of bits used to represent n and k is a constant; vice versa Shor's algorithm runs in O(b3log b) time, and it uses O(b2log n log log n) uantum gates. Another significant example of quantum advantage is provided by the Grover's quantum algorithm that searches an unstructured unordered list with N entries, for a marked entry, using only O(√N) queries instead of the O(N) queries required classically [2]. These improvements in computational performance are made possible by massive and intrinsic parallelism that arises from the use of quantum mechanical effects known as superposition, entanglement, and interference. Research in quantum computing is particularly important because this paradigm is no longer a theoretical utopia, as real quantum computers can now be accessed and programmed through cloud-based approaches, and anyone can try their hand at implementing new or established quantum algorithms. In this innovative scenario, the recent implementation of quantum algorithms for machine learning, optimization, and reasoning has led to show how quantum computers could solve problems in the field of artificial intelligence more efficiently than their classical counterparts [3][4][5]. A major advantage of quantum computing applied to machine learning is the exponential increase in the number of dimensions that can be processed, compared to classical machine learning algorithms [6]. For example, while a classical artificial neuron can process an input of N dimensions, a quantum perceptron can process 2N dimensions, which can significantly speed up the running time of both training and classification/regression algorithms [7]. In addition, [8] shows that quantum computers could provide improved performance in running evolutionary algorithms, bio-inspired optimization methods currently used in various application domains, such as training machine learning models. Again, [9] shows that quantum computers can provide a quantum advantage in running inference engines based on linguistic fuzzy rules, making it possible to use quantum devices as efficient decision frameworks. In addition to using quantum computers to improve the performance of artificial intelligence techniques, the synergy between these two research areas can also be exploited in the opposite direction, where artificial intelligence supports the design of quantum technologies. In fact, quantum computers are living their first steps of life, the so-called Noise Intermediate-Scale Quantum (NISQ) era, where quantum devices are characterized by reduced computational capabilities and affected by computational noise. In these egative scenarios, artificial intelligence methods can enable the design of appropriate strategies to address the above issues and make quantum computers more feasible for use in real-world applications. Some examples of these artificial intelligence approaches to quantum computing are those related to quantum error mitigation, quantum circuit mapping, quantum transpiling, and so on. For example, [10] and [11] use an unsupervised machine learning technique and a bio-inspired optimization algorithm, respectively, to mitigate the effects of quantum errors in computation. In [12], deep neural networks are used to address the problem of quantum circuit mapping, i.e., enabling the execution of a generic quantum circuit on a quantum processor characterized by a specific topology. Moreover, in [13] and in [14] the transpilation of quantum circuits implementing the Quantum Approximate Optimization Algorithm (QAOA) has been addressed using genetic algorithms and AI planning, respectively. Finally, in [15], quantum circuits implementing important quantum algorithms such as the Quantum Fourier Transform (QFT) or Grover's algorithm have been compiled using the Ant Colony Optimization algorithm. Consequently, it is clear that artificial intelligence and quantum computing can benefit from each other and open up a new research direction in computer science. The strong interest in the integration of quantum computing and artificial intelligence is further evidenced by the growing number of papers published since 2012 , as shown in Figure below.
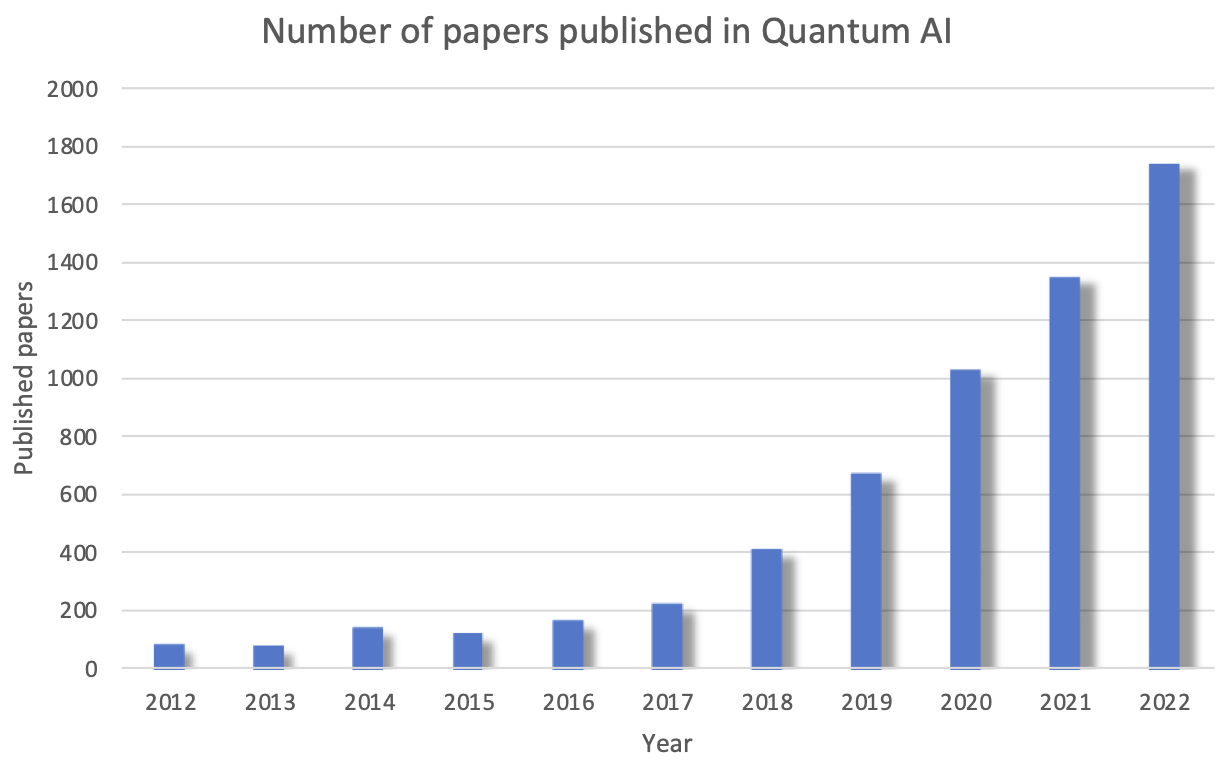
However, despite the strong interest of the scientific community in the synergistic field of quantum computing and artificial intelligence, this research area lacks a scientific forum dedicated to the discussion and management of research activities in this area. For this reason, we are pleased to launch an initiative to organize a research network in Quantum Artificial Intelligence under the umbrella of the IEEE Computer Society. This newsletter is part of this initiative, as well as the organization of the Workshop on Quantum Artificial Intelligence (QAI) 2023, a first event on the topic that we are organizing in Naples, Italy.
References
[1] P. W. Shor, "Algorithms for quantum computation: discrete logarithms and factoring," 35th Annual Symposium on Foundations of Computer Science. IEEE Computer Society Press, 1994, pp 124-134.
[2] L. K. Grover, "A fast quantum mechanical algorithm for database search," 28th annual ACM symposium on the theory of computing, 1996, p 212.
[3] J. Biamonte , P. Wittek, N. Pancotti, P. Rebentrost, N. Wiebe, S. Lloyd, "Quantum machine learning," Nature, vol. 549, 2017, pp. 195-202.
[4] V. Dunjko, H. J. Briegel, "Machine Learning & Artificial Intelligence in the Quantum Domain: a Review of Recent Progress," Report on Progress in Physics, vol, 81, no. 7, 2018.
[5] M. Schuld, F. Petruccione, "Supervised Learning with Quantum Computers," Quantum Science and Technology, Springer International Publishing, 2018.
[6] V. Havlicek, A. D. Corcoles, K. Temme, A.W. Harrow, A. Kandala, J. M. Chow, J. M. Gambetta (2019), "Supervised Learning with Quantum-Enhanced Feature Spaces," Nature, vol. 567, no. 7747, 2019, pp. 209-212.
[7] F. Tacchino, C. Macchiavello, D. Gerace, D. Bajoni, "An artificial neuron implemented on an actual quantum processor," npj Quantum Information, vol. 5, 2019.
[8] G. Acampora, A. Vitiello, "Implementing evolutionary optimization on actual quantum processors," Information Sciences, vol. 575, 2021, pp. 542-562.
[9] G. Acampora, R. Schiattarella and A. Vitiello, "On the Implementation of Fuzzy Inference Engines on Quantum Computers," in IEEE Transactions on Fuzzy Systems, 2022.
[10] G. Acampora and A. Vitiello, "Error Mitigation in Quantum Measurement through Fuzzy C-Means Clustering," 2021 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Luxembourg, Luxembourg, 2021, pp. 1-6, doi: 10.1109/FUZZ45933.2021.9494538.
[11] G. Acampora, M. Grossi and A. Vitiello, "Genetic Algorithms for Error Mitigation in Quantum Measurement," 2021 IEEE Congress on Evolutionary Computation (CEC), Krakow, Poland, 2021, pp. 1826-1832.
[12] G. Acampora, R. Schiattarella, "Deep Neural Networks for Quantum Circuit Mapping," Neural Computing and Applications, vol. 33, 2021, pp. 13723-13743.
[13] L. Arufe, M. A. Gonzalez, A. Oddi, R. Rasconi, R. Varela, "Quantum Circuit Compilation by Genetic Algorithm for Quantum Approximate Optimization Algorithm Applied to Maxcut Problem," Swarm and Evolutionary Computation, vol. 69, 2022.
[14] K. Booth, M. Do, J. Beck, E. Rieffel, D. Venturelli, and J. Frank, "Comparing and Integrating Constraint Programming and Temporal Planning for Quantum Circuit Compilation," 28th International Conference on Automated Planning and Scheduling, 2018.
[15] T. Atkinson, A. Karsa, J. Drake, J. Swan, "Quantum Program Synthesis: Swarm Algorithms and Benchmarks," European Conference on Genetic Programming, 2019, pp. 19-34.
